If you were asked to perform an enlargement, what would you know about the scale factor?

Related Pages
Scale Cistron & Shapes
Scaling and Area
Surface area of Similar Figures
Grade 8

Scale Factor

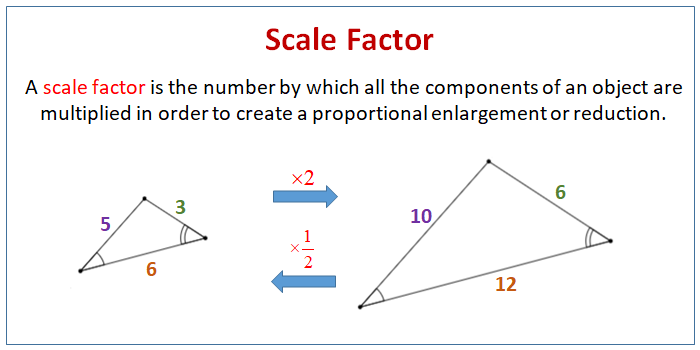
A scale factor is the factor by which all the components of an object are multiplied in club to create a proportional enlargement or reduction.

The following diagram shows an example of scale factor. Scroll downwardly the folio for more examples and solutions on how to utilize scale factors.

How to use calibration to determine the dimensions of a proportional model?

Define scale gene.
Scale cistron is similar to a unit calibration except no units are given. Scale factor is a ratio comparing the scaled measurement to the actual measurement.

How to use scale factor to sketch a proportional scale model?

Instance:

1. The scale cistron of a model automobile is 1:24. If the actual automobile is xviii ft long and 8 ft broad, how long and wide will the model car exist in inches?
2. You need to sketch a ladybug using a scale gene of 12. If a ladybug is eight mm long and iv mm wide, what volition be the length and width of the sketch be in cm?

• Show Video Lesson

A brief form in scale cistron for similar geometric figures
Scale Cistron is defined as the ratio of whatsoever two corresponding lengths in two like geometric figures.
Like Figures are figures such that:

1. Respective angles are congruent.
2. Respective side lengths are proportional.

• Prove Video Lesson

Ratio Of Perimeters And Areas

This video explains how to find the ratio of areas and ratios of perimeters for similar polygons.

Ratio of perimeters = ratio of sides
Ratio of areas = (ratio of sides)^two

• Show Video Lesson

Calibration Factor/Perimeter Ratio/Surface area Ratio

Example:
Given that the polygon in each pair are similar. Find the scale factor, perimeter ratio and area ratio.

• Show Video Lesson

Areas and Perimeters of Like Figures
This video discusses how to find the ratio of the perimeters and the ratio of the areas of similar figures from the scale factor. Likewise how to utilize these ratios to detect missing perimeters and areas.

If the scale factor of 2 similar figures is a/b, so

1. the ratio of their perimeters is a/b and
2. the ratio of their areas is a²/b²

Examples:

1. The trapezoids at the correct are similar. The ratio of the lengths of corresponding sides is 6/nine or ii/three.
   a) What is the ratio (smaller to larger) of the perimeters?
   b) What is the ratio (smaller to larger) of the areas?
2. 2 similar polygons have corresponding sides in the ratio v:seven.
   a) What is the ratio (larger to smaller) of their perimeters?
   b) What is the ratio (larger to smaller) of their areas?
3. The expanse of the smaller regular pentagon is about 27.5 cmii. What is the best approximation for the area of the larger regular pentagon?<
4. If the area of the smaller triangle is near 39 ft², what is the expanse of the larger triangle to the nearest tenth?
5. The triangles are similar. What is the scale cistron? What is the ratio of their perimeters?
6. The areas of ii similar rhombuses are 48m² and 128m². What is the ratio of their perimeters?

• Show Video Lesson

How does scale factor impact side lengths, perimeter, expanse, and angles?
If the scale factor from A to B is x then
The side lengths of B will exist x times larger than A
The perimeter of B will be x times larger than A
The area of B will be 10ⁱⁱ times larger than A
A and B volition have the aforementioned shape and angles.

• Evidence Video Lesson

Ratio Of Surface Areas And Volumes

Scale Factor, Length, Surface area and Book for similar shapes
Ratio of lengths = ratio of sides = scale gene
Ratio of surface areas = (ratio of sides)^two = (scale gene)²
Ratio of volume = (ratio of sides)ⁱⁱⁱ = (scale factor)^three

Surface Areas And Volumes Of Similar Solids
Similar solids accept the same shape, and all their corresponding dimensions are proportional.
If the scale factor of ii similar solids is a:b, then
• the ratio of their corresponding areas is aⁱⁱ:bⁱⁱ
• the ratio of their volumes is a³:b³

Examples:

1. Are the two rectangular prisms similar? If so, what is the scale factor of the first figure to the 2nd figure?
2. The square prisms at the right are like. What is the scale factor of the smaller prism to the larger prism?
3. What is the scale cistron of 2 similar prisms with surface areas 144 thouⁱⁱ and 324 m²?
4. The volumes of two like solids are 128 thousand³ and 250 mⁱⁱⁱ. The surface surface area of the larger solid is 250 k². What is the surface surface area of the smaller solid?

• Show Video Lesson

Similar Figures, Calibration Factor, Area & Volume Ratios

Examples:

1. The calibration factor between 2 similar figures is given. The surface surface area and volume of the smaller figure are given. Find the expanse and volume of the larger figure.
   Scale factor v:half-dozen
   SA: 275 cm²
   V: 3000 cmⁱⁱⁱ
2. Some information near the surface area and volume of two like solids has been given. Detect the missing value.

• Testify Video Lesson

3D Figures - Scale Models and Factors

Learn most scaling 3D figures using scale cistron
Problem: A 6 cm by 2 cm rectangular prism is congenital form small rectangular prisms of length 3 cm.
a) What is the scale gene from the smaller to the larger model?
b) Discover the width and height of the smaller rectangular prisms.
c) Compare the surface area of the two rectangular prisms.
d) Compare the book of the two rectangular prisms.

Endeavor the free Mathway reckoner and problem solver beneath to exercise various math topics. Endeavor the given examples, or type in your ain problem and check your reply with the step-by-step explanations.

Nosotros welcome your feedback, comments and questions about this site or folio. Please submit your feedback or enquiries via our Feedback page.

lundtoply1985.blogspot.com

Source: https://www.onlinemathlearning.com/scale-factor.html

Share this post